南开团队破解百年数学难题"卡拉比猜想"关键环节
一、北师大"AI+教育"核心成果的国际影响力
联合国教科文组织人工智能与教育教席
北师大与联合国教科文组织合作设立的教席,聚焦教育领域人工智能研究、培训与资源共享,通过发起国际联合研究计划(如人机协作教学场景应用)、招募全球访问学者及博士后,推动AI+教育国际人才培养。该教席已构建跨国合作网络,覆盖亚洲、非洲、美洲等地区,为全球教育创新提供理论支持与实践范式。
《智慧教育:迈向教育2050的路径》著作发布
在2025全球智慧教育大会上,北师大团队发布该书,系统探讨智慧教育如何成为2050年全球教育目标。书中提出的"三新"(数字化迈向智慧教育新阶段、能力为本的人才培养新标准、未来教育变革新路径)和"四未来"(培养未来教师、打造未来课堂、建设未来学校、创建未来学习中心)框架,为国际教育界提供前瞻性指导,间接影响全球教育政策制定。
AI+循证教研赋能"双新"模式
北师大联合基础教育教材综合研究国家教材建设重点研究基地,通过AI"大先生"智能系统助力课程实施与教学变革。该模式已吸引20多个联盟区域和200余所联盟学校参与,汇集逾千个课例,形成可复制的AI+教研方案,为全球教育创新提供实践样本。
二、北师大成果与全球教育创新峰会的间接关联
世界教育创新峰会(WISE)的定位与北师大成果的契合性
WISE峰会以推广优秀教育模式、利用创新实现未来教育全面发展为核心目标。北师大在AI+教育领域的成果(如智慧教育框架、AI+循证教研模式)与峰会宗旨高度契合,其研究成果可通过峰会平台进一步辐射至全球。
北师大成果对全球教育创新的推动作用
技术输出:北师大通过教席、联合研究计划等,向中东欧、东南亚、非洲国家输出AI+教育技术,如暑期学校项目面向全球中学生开展设计、计算、创新思维培训。
标准制定:其提出的智慧教育发展框架和AI能力框架,为国际教育界提供参考,影响全球教育数字化转型路径。
实践示范:AI+循证教研模式在联盟学校的成功应用,为发展中国家提供低成本、高效益的教育创新解决方案。
三、北师大"AI+教育"成果的未来国际合作展望
深化与WISE峰会的合作
北师大可通过参与WISE教育项目奖评选、主办分论坛等形式,直接展示其AI+教育成果。例如,将AI+循证教研模式申报WISE教育项目奖,或联合峰会发布《全球智慧教育发展报告》。
拓展国际合作网络
依托教席的跨国合作基础,北师大可与更多国家的教育机构共建联合实验室,开展AI+教育实证研究。例如,与非洲国家合作开发本土化AI教学工具,解决教育资源不均衡问题。
推动全球教育治理
北师大可借助其国际影响力,参与制定AI+教育的全球标准与伦理框架。例如,在联合国教科文组织框架下,牵头起草《AI教育应用国际指南》,规范技术使用边界。
卡拉比猜想在物理学中有何应用?
一、核心机制:卡拉比-丘流形与超弦理论的维度匹配
超弦理论的维度需求
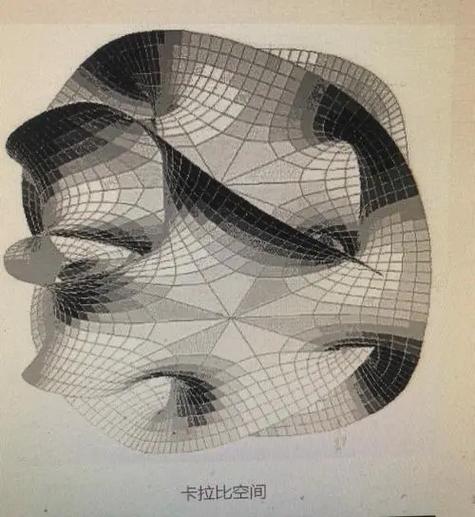
超弦理论要求宇宙存在10维时空(4维可见时空+6维额外维度),而卡拉比-丘流形(实维度6)恰好满足这一条件。其紧致化过程通过将6维空间“卷曲”至普朗克尺度(半径小于米),解释了为何人类仅感知到4维时空。
里奇平坦性与物理场的一致性
卡拉比-丘流形的里奇平坦性(Ricci-flat)意味着其曲率张量处处为零,但通过爱因斯坦场方程,在无物质分布()时,曲率仍可由引力场本身产生。这一特性与广义相对论中“时空告诉物质如何运动,物质告诉时空如何弯曲”的哲学高度契合,为暗物质存在提供了数学依据。
二、理论突破:超对称性保持与粒子谱生成
超对称性部分保持
卡拉比-丘流形的全纯性结构在紧致化过程中可保持四分之一的超对称性,这是构建现实物理模型的关键。若超对称性完全破坏,理论将失去预测能力;而完全保持则与实验观测矛盾,卡拉比-丘流形提供了平衡点。
粒子谱与拓扑不变量的关联
卡拉比-丘流形的拓扑不变量(如Hodge数)直接决定低能物理中的粒子谱。例如,Hodge数和分别对应规范玻色子和手性费米子的数量,为标准模型中的粒子分类提供了几何解释。
三、技术延伸:几何流与模空间研究
几何流方程的应用
卡拉比猜想的证明推动了Kähler-Ricci流等几何流方程的研究,这些方程在寻找特殊度量(如卡拉比-丘度量)和分析流形奇点形成中发挥重要作用。例如,通过求解热方程逼近调和形式,可数值构造卡拉比-丘流形的具体例子。
模空间结构的探索
卡拉比-丘流形的模空间(复结构模空间与Kähler结构模空间的乘积)研究揭示了不同流形之间的变形关系。SYZ猜想进一步提出,每个卡拉比-丘流形应允许特殊的Lagrangian纤维化,为理解镜像对称性提供了几何图像。
四、跨学科影响:从数学到物理的桥梁
卡拉比猜想的证明不仅解决了数学难题,更展示了数学严格性与物理直观的结合。其方法论(如将几何问题转化为非线性偏微分方程、建立先验估计)被广泛应用于代数几何、量子场论等领域。例如,镜像对称猜想中卡拉比-丘流形的对偶性成为关键工具,而广义卡拉比流的研究则深化了对几何结构演化的理解。





评论列表